When the morning surf is good, Steve Shkoller heads to the ocean waters near his home in Marin. He paddles out into the big blue, his body and board bobbing with the water beneath him, and then he waits. For the mentally and physically active Shkoller, that space between the waves is a place of tranquility. 

“You’re so relaxed and there’s a kind of calmness,” said Shkoller, a professor in the Department of Mathematics at UC Davis. “Important ideas sometimes emerge from that state of complete calm.” 

Since childhood, Shkoller has organized his life around two things: surfing and mathematics. And those two facets of his life share something in common: waves. 

In his research, Shkoller aims to illuminate the mathematical underpinnings of shockwave formation and fluid dynamics. He’s specifically interested in developing both geometric and analytical tools that mathematically explain the multidimensional behavior of shockwaves. 

Shockwaves form from steepening sound waves, which are modeled by the Euler equations, centuries-old “conservation laws’’ that govern the flow of fluids such as water and air, among others.   

“Solutions to the Euler equations of fluid dynamics explain how airplanes fly and how blast waves propagate, but also the same equations are fundamental to weather prediction and global climate change, and describe the motion of astrophysical bodies such as gaseous stars and in fact, the expansion of the universe.” — Shkoller  

Exploring shockwave formation

While the Euler equations are pervasive in nature and engineering, mystery surrounds the mathematics behind them. The phenomena of shock formation occur in a highly non-linear regime in which fast-moving sound waves interact with possibly turbulent vortex motion to create new wave patterns with highly non-trivial geometry. A small change in direction or shape of any of the propagating waves can have a profound effect on the resulting interaction.

Because of this, mathematicians have only developed a complete theory for shockwave motion in one space dimension, where the geometry is trivial. 

“As hard as people have tried, and many people have tried, the success of the one-dimensional theory cannot be generalized to the physical three-dimensional space that we live in. One of the biggest open questions in the field of Partial Differential Equations is:  how can one prove the existence of a unique shockwave solution in multiple space dimensions?” — Shkoller 

Shkoller hopes to provide an answer. 

“We know that for the Euler equations, we cannot have global existence of smooth solutions because shocks form in finite time,” he said. “Not only do shocks form, but there are other discontinuities that can develop.” 

When Shkoller runs multidimensional fluid dynamic simulations that recreate the propagation of sound, shockwaves eventually form in the simulation. 

“Imagine being in line for a movie and the people in front of you are going slower than you; you’re going to end up bumping into the person in front of you,” Shkoller said. 

In essence, this is what happens with the particles in Shkoller’s simulations. They move in waves. 

“The particles are going really fast and the ones in front of them are slowing down,” Shkoller said. “When they collide, a shock forms.” 

In Shkoller’s analysis, this collision manifests as an infinitely steep incline that denotes a singularity known as a gradient catastrophe or shock. 

“This kind of thing is ubiquitous and happens all the time,” Shkoller said. “When you’re flying in a modern passenger jet, air is accelerated over the top of the wing resulting in a visible shock wave, and when the space shuttle reenters the atmosphere there is an incredibly strong cone-shaped shock whose apex is at the nose of the shuttle.” 

While this natural wave steepening phenomenon is widespread and can be visualized in computational models, it’s much more difficult to capture mathematically. But recently, Shkoller and his collaborator Vlad Vicol of New York University proved a theorem that provides a detailed description of shock formation for the Euler equation in multiple space dimensions.

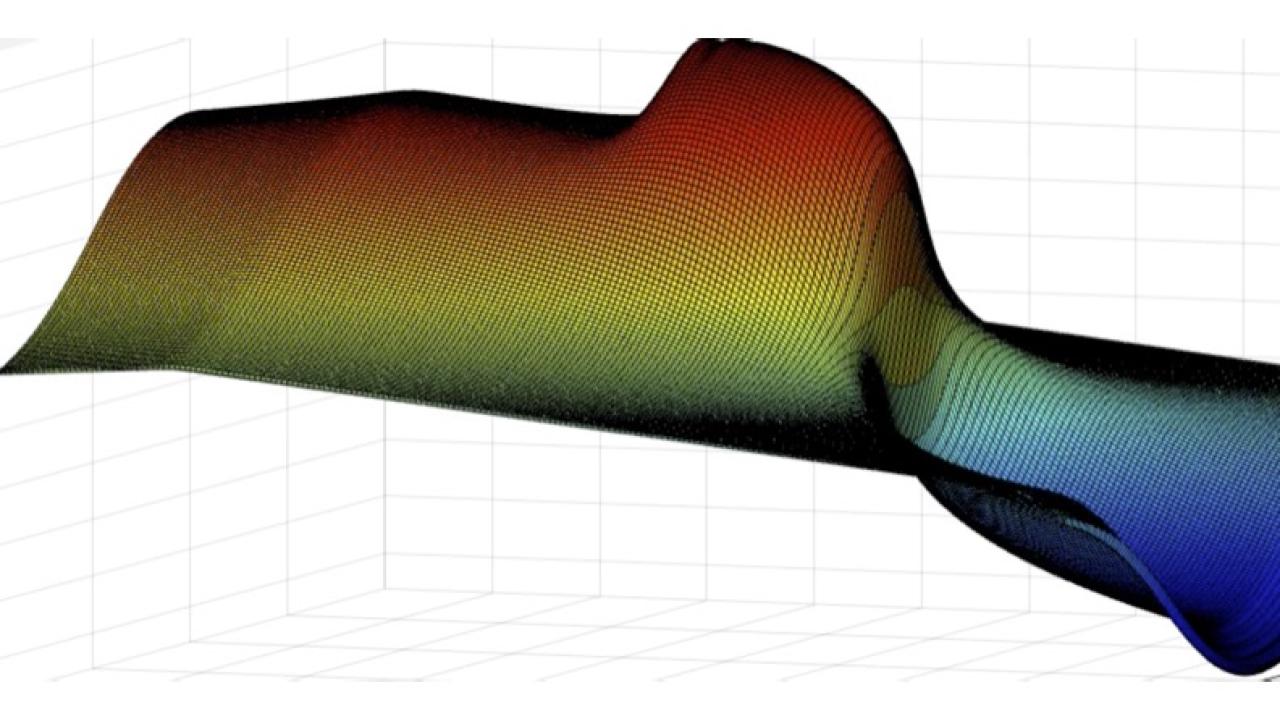
Riding the singularity

Shkoller recently discussed his program’s research progress at the 2024 International Congress of Mathematical Physics, held in Strasbourg, France. Shkoller was a plenary speaker at the conference. 

“Our recent developments have devised new geometric analysis tools that have allowed us to study the structure of singularity formation in multiple space dimensions with complicated geometric wave patterns and to understand how to uniformly estimate solutions to Euler,” he said. 

Such analytical advancements are likely to improve the numerical methods for computationally simulating the Euler equations, which, in turn, could lead to innovations in astrophysical computations as well as long-range weather prediction here on Earth. 

But the math takes time, potentially even years. For Shkoller, providing existence of such unique shockwave solutions would be akin to catching the perfect wave as a surfer. 

“The best wave you can get as a surfer is what’s called getting barreled, where the wave pitches over you and the crest falls in this cylindrical shape. You’re inside that cylindrical tube and then the wave crashes and when that wave crashes, that’s a singularity.” — Shkoller 

All photos and graphics courtesy of Steve Shkoller